Sample Space And Events

A going into a room and turning on a light.

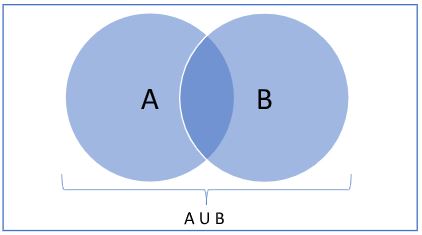
Sample space and events. A compound event is the selected card is red there are 26 red cards and so there are 26 simple events comprising the compound event 4. An outcome is in ef if it is either in e or. Sample space and events sample space. It is common to refer to a sample space by the labels s w or u for.

This feature is not available right now. Rolling an ordinary six sided die is a familiar example of a random experiment an action for which all possible outcomes can be listed but for which the actual outcome on any given trial of the experiment cannot be predicted with certaintyin such a situation we wish to assign to each outcome such as rolling a two a number called the probability of the outcome. Sample space and eventsbr if two events have no element in common they are called mutually exclusive events ie. A subset of the sample space.

Full lessons complete with extra examples downloads and quizzes searchable and jumpable topics to save you time ability to ask questions to instructor and other students. Which of the follow are experiments. Identify the sample space give an example of a simple event and a compound event. Flip a coin twice.

Defines experiment outcome sample space and event. Flip a coin twice and the two results are different. In probability theory the sample space also called sample description space or possibility space of an experiment or random trial is the set of all possible outcomes or results of that experiment. Sample spaces and events.

Select a driver randomly from all drivers in the age category of 18 25. D driving a car up and down the. Section 71 experiments sample spaces and events experiments an experiment is an activity with observable results. Definitions of sample space event union intersection and complement.

C flipping a coin and observing wether the coin lands on heads or tails. B rolling a die and observing the number that appears on the uppermost face. A sample space is usually denoted using set notation and the possible ordered outcomes are listed as elements in the set. Please try again later.

They cannot occur simultaneouslybr in above example r t are not mutually exclusive events while r u and t u are mutually exclusive eventsbr in order to discuss the basic concepts of the probabilistic model which we wish to develop it will be very convenient to. Rolling an ordinary six sided die is a familiar example of a random experiment an action for which all possible outcomes can be listed but for which the actual outcome on any given trial of the experiment cannot be predicted with certaintyin such a situation we wish to assign to each outcome such as rolling a two a number called the probability of the outcome. The outcome is even 246. The set of all possible outcomes.